Erv Wilson Diagrams
Info
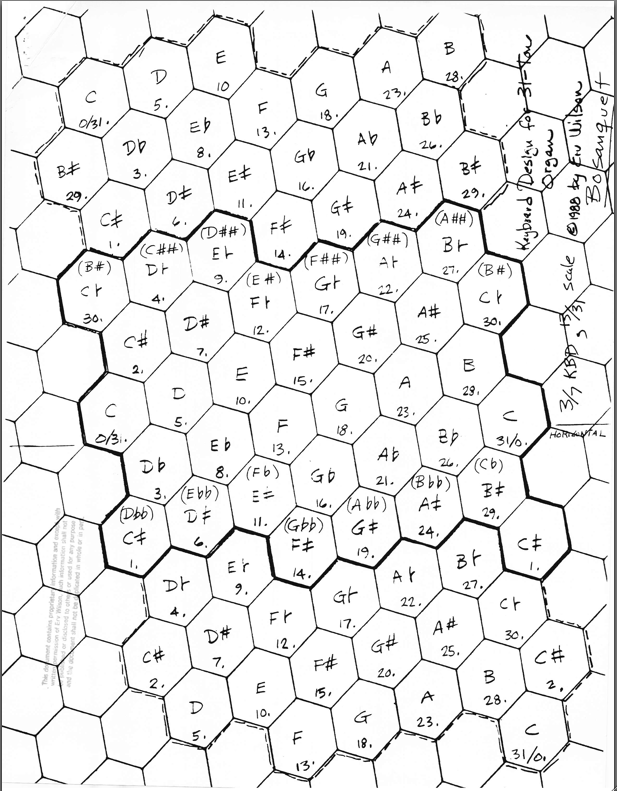
A diagram of how to map a 31 tone scale onto Erv Wilson’s hexagonal keyboard. (Also see Starr Labs)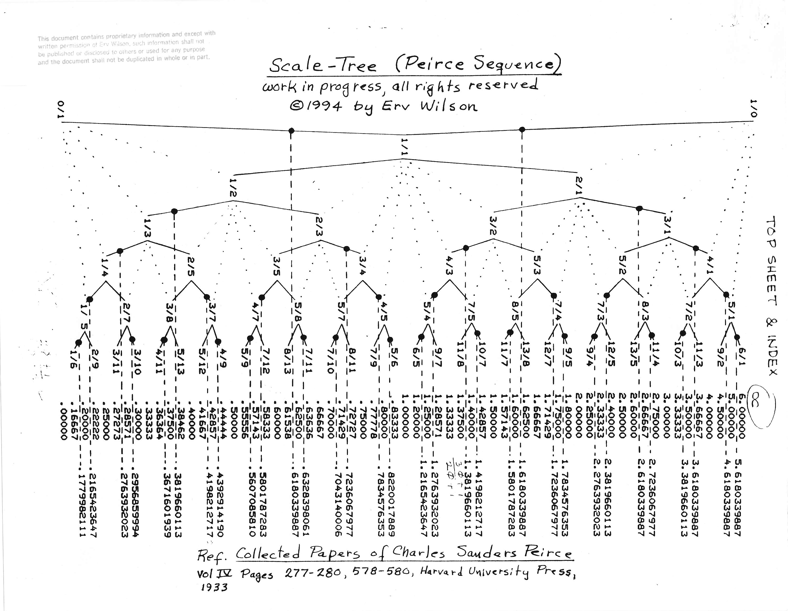
The first page of the pitch field known as The Scale Tree, aka Moments of Symmetry. Those fractions, or their decimal equivalents, generate a vast array of unequally tempered scales that all possess the characteristic of containing only two different sized chromatic intervals (instead on just one as per the regular western piano tuning). These scales make for the most exotic melodies!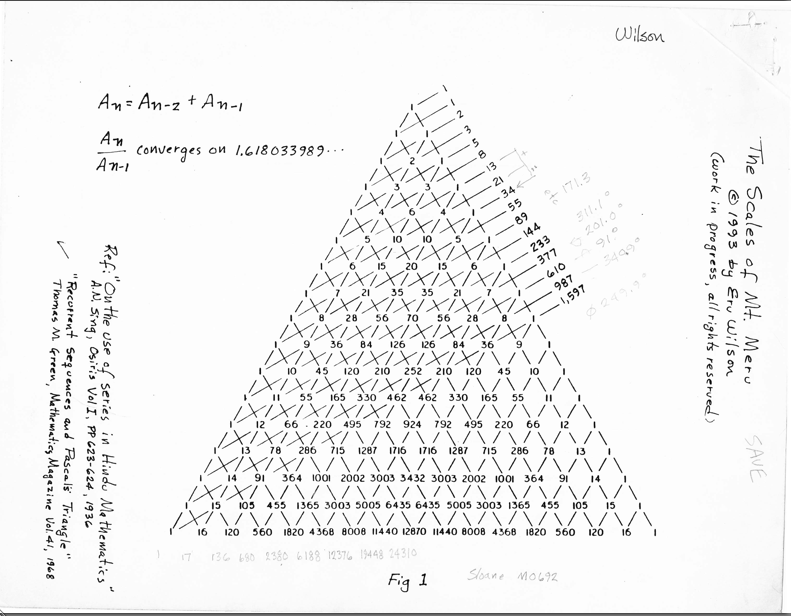
Also know as the scale of Mt. Meru, Pascal’s triangle provides a way of deriving sets of musical scale frequencies by adding the diagonals of this ancient array. Coincidentally, many of them resemble scales used in many of the world’s indigenous cultures.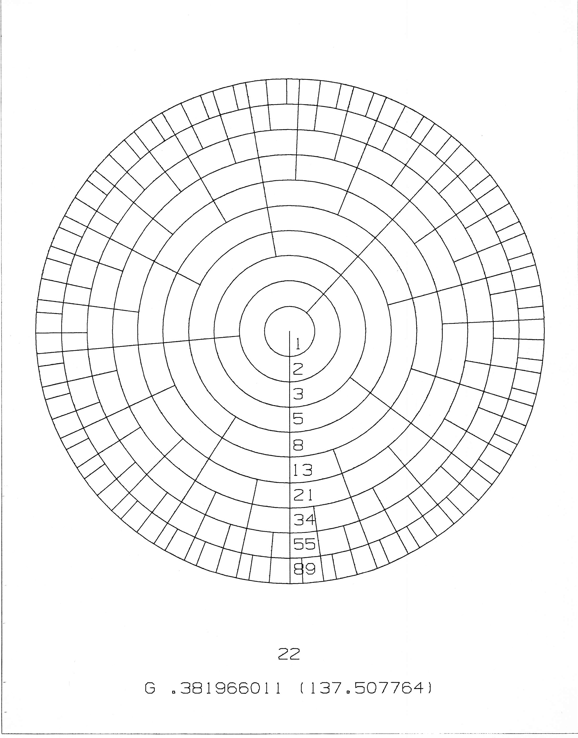
This is a circular version of a set of scales found on the Scale Tree. This one generates the “Golden Mean” and can be used for scales, rhythms, and visual art. These circular transforms of the Scale Tree Erv calls “Holograms”, due to the fact that they look like an unusual clock.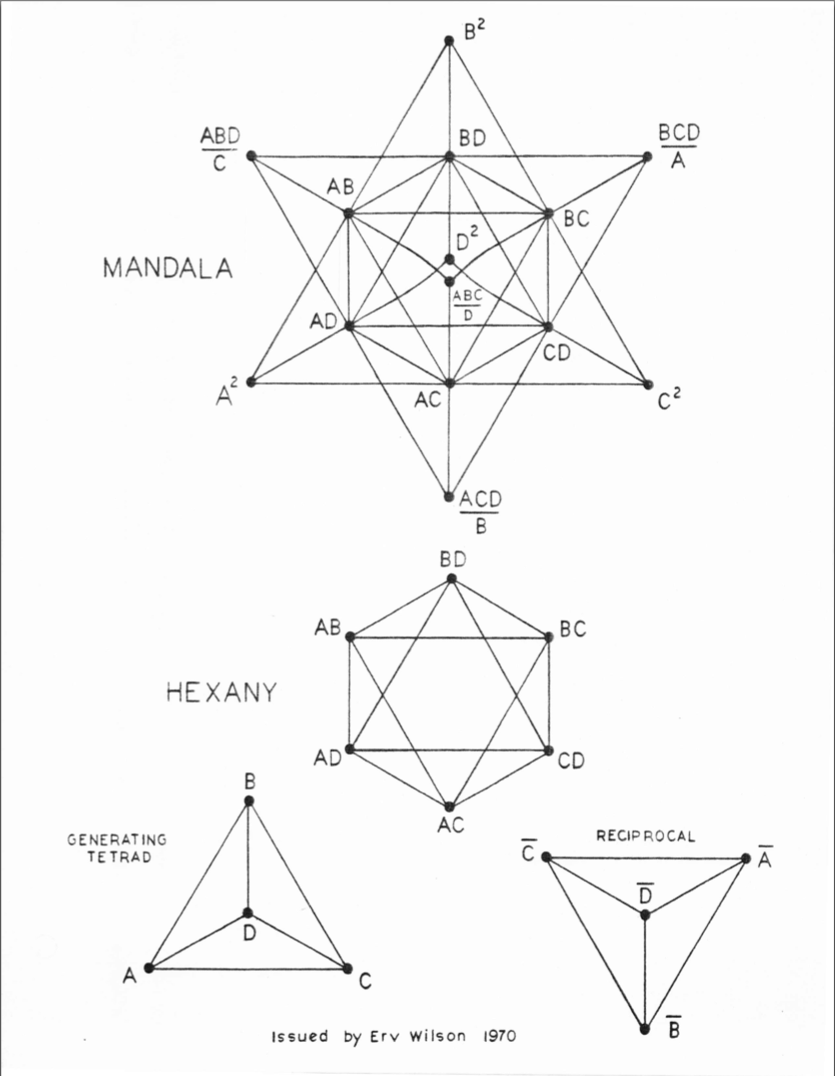
A prime example of one of Erv’s ways of creating new scales. He call this approach here “Combination Product Sets.” By multiplying a small set of numbers (any numbers, here represented by the letters A-D), you can create a larger group of derivative notes, Here he maps the note relationships onto geometric objects.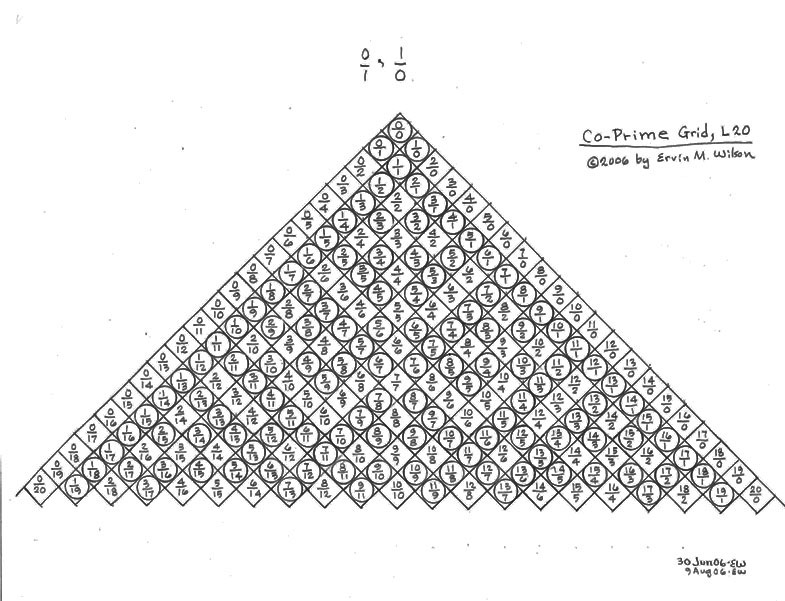
An arithmetic array of fractions seeded with any two a starting values at the top. The circled numbers are spots where the numerator and denominator are “coprime” to each other, i.e. the only number that can divide equally into both is “1”.
To view the entire collection of Wilson’s papers go to http://www.anaphoria.com/wilson.html
31 Tone Hex Keyboard

A diagram of how to map a 31 tone scale onto Erv Wilson’s hexagonal keyboard. (Also see Starr Labs)
The Scale Tree

The first page of the pitch field known as The Scale Tree, aka Moments of Symmetry. Those fractions, or their decimal equivalents, generate a vast array of unequally tempered scales that all possess the characteristic of containing only two different sized chromatic intervals (instead on just one as per the regular western piano tuning). These scales make for the most exotic melodies!
Pascal’s Triangle

Also know as the scale of Mt. Meru, Pascal’s triangle provides a way of deriving sets of musical scale frequencies by adding the diagonals of this ancient array. Coincidentally, many of them resemble scales used in many of the world’s indigenous cultures.
Horogram 22

This is a circular version of a set of scales found on the Scale Tree. This one generates the “Golden Mean” and can be used for scales, rhythms, and visual art. These circular transforms of the Scale Tree Erv calls “Holograms”, due to the fact that they look like an unusual clock.
Hexany

A prime example of one of Erv’s ways of creating new scales. He call this approach here “Combination Product Sets.” By multiplying a small set of numbers (any numbers, here represented by the letters A-D), you can create a larger group of derivative notes, Here he maps the note relationships onto geometric objects.
The Coprime Grid

An arithmetic array of fractions seeded with any two a starting values at the top. The circled numbers are spots where the numerator and denominator are “coprime” to each other, i.e. the only number that can divide equally into both is “1”.



No Comments yet
Be the first to write a comment